阪大数学(文系)
解くべき問題を見極める力と標準問題を解き切る力が必要!
傾向
出題形式
試験時間は90分、3問形式
3か年の傾向について
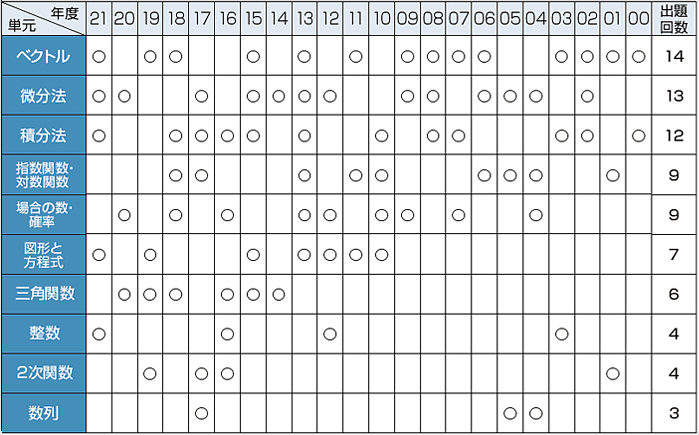
ここ3か年の頻出単元は「ベクトル」、「微分法」、「平面図形と式」、「三角関数」です。また、2000年からの出題単元で見ても「ベクトル」、「微分法」、「積分法」が突出しています。
過去に出題された単元の頻度
問題の難易度は年によってかなり上下がありますが、大抵は教科書や問題集ではあまり見慣れない問題(いろいろな単元が融合しているものが多い)や計算が煩雑な問題が出題されています。まずは手を動かしてみて、知っていることといかに結び付けて考えるかが大事になります。また3問の中で必ず解くべき問題と、部分点狙いでよい問題の見極めができることも求められています。定石解法は確実に定着させておく必要があります。
